显因子模型简介
本文共 2353 字,大约阅读时间需要 7 分钟。
SiGIR 2014在推荐系统方面收录了三篇很有价值的论文,提出了新的算法框架。在此介绍第一种算法框架(来自论文:Explicit Factor Models for Explainable Recommendation based on Phrase-level Sentiment Analysis,基于短语级情感分析的可解释型推荐模型——显因子模型)。如与本文有不同理解,不吝赐教。
一、概述
EFM ( Explicit Factor Models,显因子模型),是针对LFM (Latent Factor Models,隐因子模型) 的不足而设计的。
LFM的特点如下:
a. 通过分类抽象出隐因子空间。在分类过程中,我们不需要关心分类的角度,结果都是基于用户打分自动聚类的。分类的粒度通过设置LFM的最终分类数来控制。
b. 对于每个物品,并不是明确地划分到某一类,而是计算其属于该类的程度。
c. 对于每个用户,计算他对每个类的兴趣度。
不足在于:
<1>单一的打分不能反映用户对物品各项特征的偏好,没有利用到用户评论。
<2>因为类别是抽象出来的,没有明确的含义,所以向用户推荐物品时,无法解释推荐理由。
EFM的特点如下:
a. 通过对用户评论进行phrase-level(短语级)的情感分析,显式地抽取物品的特征和用户的意见。
b. 对于每个物品,计算它对每个特征的包含程度。
c. 对于每个用户,计算他对每个特征的喜好程度。
d. 根据用户评论和打分两方面的数据(设置这两者的权重),计算得到用户-物品的喜好程度矩阵。
e. 向用户推荐购买物品的同时,也建议用户不要购买某些物品。
优点在于:
<1>充分利用用户评论,提高算法的精准度。
<2>因为物品的特征已经被显式的抽取出来,所以向用户推荐商品时,可以直观地解释推荐理由。从而帮助用户更快决定是否购买;特别是建议用户不要购买某些物品,有助于提高用户对系统的信任度。
二、EFM算法框架
1. 构建情感词典
EFM构建词典的过程用下面的例子说明:(有 阴影的格子表示用户对该物品进行了评论。)
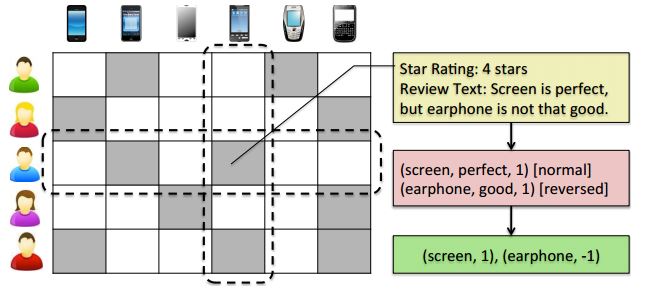
首先,从用户评论的 语料库抽取物品的特征(或者说,物品的某一方面):screen、earphone。然后,抽取用户对这些特征的意见:perfect、good。如果这些表示意见的 词汇本身是积极的情感,则用1表示;反之则用-1表示。所以在这个例子中,情感短语表示为(screen, perfect, 1), (earphone, good, 1),这一条条短语就组成了情感词典。
根据情感词典,对用户评论进行情感分析, 判断用户的情感是肯定的还是否定的。例如:perfect是肯定的,而good是否定的,因为前面加了否定词not。所以,这个例子中,用户的评论就可以表示成 特征/情感对:(screen, 1), (earphone, -1)。
把用户的评论表示为 特征/情感对,是构建情感词典的目的。
2. 构建矩阵
EFM需要构建三个矩阵。
第一个是 用户打分矩阵A,表示第 i 个用户对第 j 个物品打的分数。由于用户不一定对所有物品都打过分数,所以没打分则记为 零。
第二个是 用户-特征关注矩阵X,表示第 i 个用户对第 j 个特征的喜好程度:
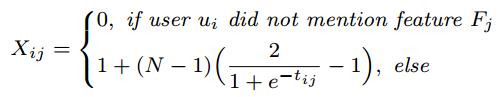
其中,N表示用户打分的最高分数(一般为5分)。为了使该矩阵的每个值与用户打分矩阵的值范围都是[1, N],用sigmoid函数规范参数的取值。
第三个是 物品-特征质量矩阵Y,表示第 i 个物品包含第 j 个特征的程度:
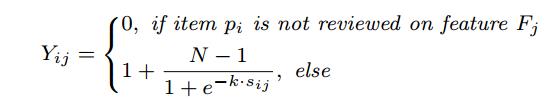
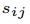 。
。 3. 估计矩阵X、Y、A的缺失值
矩阵X、Y中的非零数表示已有的用户或物品与特征之间的关系,而 零则表示尚未清楚的 缺失值。为了估计这些缺失值,则采用 最优化损失函数的方法。
损失函数是把一个事件 映射到 能表示与其相关的经济成本或机会成本的实数的一种函数。在统计学中,损失函数经常用来 估计参数。损失函数的未知参数用 θ 表示,决策的方案(已获得的实际值)用 d 表示,常见的损失函数有两种:
二次损失函数: L(θ,d) = c(θ − d)2
绝对损失函数:
该算法采用的是 二次损失函数。采用最优化损失函数的方法,是指 最小化估计值与真实值的差距。所以X、Y的最优化损失函数如下:
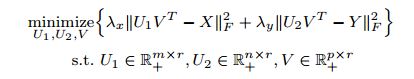
与LFM相比,EFM已经抽取出了显式的特征。我们假设一些特征属于某一类型,而用户喜欢这一类型或者物品包含这一类型,由于特征是显式的,因而引入“显因子”的概念。上面表达式中的 r 就是指显因子的数量。
同理,估计打分矩阵A的缺失值也会用到显因子。同时,考虑到 用户在打分时还会考虑到其他一些潜在的因素,因此也引入了LFM中用到的 隐因子, 用 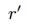 表示隐因子的数量。A的最优化损失函数为:
表示隐因子的数量。A的最优化损失函数为:
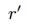 表示隐因子的数量。A的最优化损失函数为:
表示隐因子的数量。A的最优化损失函数为: 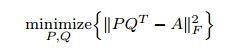
然后把这两个损失函数合并为:
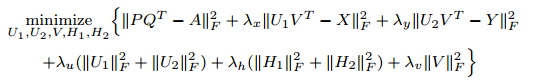 ( * )
( * ) 其中, 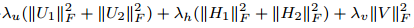 是防止过拟合的正则化项。
是防止过拟合的正则化项。
( * )式通过拉格朗日函数和KKT条件的推导后,得到矩阵V、U1、U2、H1、H2的更新公式,如下所示:
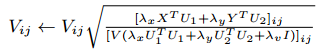
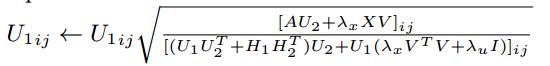
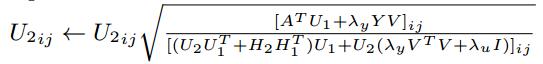
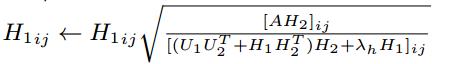
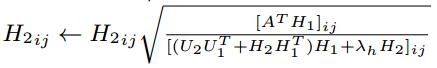
4. Top-K推荐
矢量 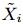 的行表示第 i 个用户对每个特征的喜好程度,选取其中 参数值最大的k个特征的下标,用
的行表示第 i 个用户对每个特征的喜好程度,选取其中 参数值最大的k个特征的下标,用 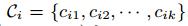 表示。然后用以下方法计算第 i 个用户对第 j 个物品的打分:
表示。然后用以下方法计算第 i 个用户对第 j 个物品的打分:
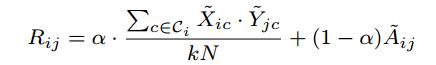
其中, 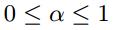 ,具体的值由实验确定。在大多数打分系统中,最高分数为5,所以N=5。
,具体的值由实验确定。在大多数打分系统中,最高分数为5,所以N=5。
最后,选择打分最高的前K个物品推荐给用户,并根据特征向用户解释推荐理由。
你可能感兴趣的文章
linux下redis安装
查看>>
量子通信和大数据最有市场突破前景
查看>>
如何申请开通微信多客服功能
查看>>
Sr_C++_Engineer_(LBS_Engine@Global Map Dept.)
查看>>
非监督学习算法:异常检测
查看>>
jquery的checkbox,radio,select等方法总结
查看>>
Linux coredump
查看>>
Ubuntu 10.04安装水晶(Mercury)无线网卡驱动
查看>>
我的友情链接
查看>>
ElasticSearch 2 (32) - 信息聚合系列之范围限定
查看>>
VS2010远程调试C#程序
查看>>
[MicroPython]TurniBit开发板DIY自动窗帘模拟系统
查看>>
从Handler.post(Runnable r)再一次梳理Android的消息机制(以及handler的内存泄露)
查看>>
windows查看端口占用
查看>>
Yii用ajax实现无刷新检索更新CListView数据
查看>>
JDBC的事务
查看>>
App 卸载记录
查看>>
JavaScript变量和作用域
查看>>
开源SIP服务器加密软件NethidPro升级
查看>>
Apache Pulsar中的地域复制,第1篇:概念和功能
查看>>